
Product: Abaqus/CAE

A design response:
is a single scalar value, such as the volume of your structure;
is calculated by the Optimization module by reading results and model data from the output database file;
can be referred to from objective functions and constraints (for example, you can create an objective function that tries to minimize the displacement at a node or a constraint that forces the weight of the structure to be reduced by at least 50%); and
is available only for certain analysis procedures (for example, you must perform an eigenvalue extraction analysis if you select a design response that tries to maximize the lowest eigenfrequencies).

The Optimization module provides a number of different design responses.
The bead height has the most significant effect on the stiffness of a shell structure that is being optimized with bead optimization. Usually, the greater the bead height the greater the stiffness, although manufacturing restrictions will limit how deep you can draw a bead. When the optimization starts, the bead height is initially zero. As the optimization proceeds, it moves the nodes in the shell normal direction until they reach the bead height. A bead height design response is available only as a constraint in a condition-based beam optimization.
| Abaqus/CAE Usage: | Optimization module: Task |
You can use the center of gravity of a selected region as a design response in an optimization. You can choose the center of gravity in the three principal directions:
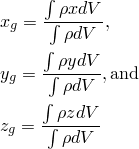
For example, you might want to constrain the center of gravity in the Y-direction so that it remains within a minimum and maximum range during the optimization. The design response can consider the center of gravity of the whole model or a region of the model.
If you select a local coordinate system, the Optimization module uses both the direction of the axes and the position of the origin to recalculate the center of gravity. The Optimization module applies the global coordinate system if you do not select a local coordinate system.
When the Optimization module calculates the center of gravity, it treats shell and membrane regions as three-dimensional regions by applying the thickness of the region. The Optimization module calculates the center of gravity using only the element types that are supported by topology optimization. As a result, the center of gravity calculated by the Optimization module might not be the same as the center of gravity calculated by Abaqus/Standard or Abaqus/Explicit; for example, if your model contains wire regions.
| Abaqus/CAE Usage: | Optimization module: Task |
Typically, you use shape optimization to modify the surface geometry of a component to minimize stress concentrations. In most cases reducing the stress levels leads to a significant increase in durability. However, it is possible that the regions of peak stress identified by a static analysis differ from the regions of maximum damage identified from a durability (or damage) analysis, and using shape optimization alone to modify the surface geometry may decrease the durability. To avoid this situation, you can incorporate a durability solver in the optimization loop to ensure that you are both reducing stress levels and increasing durability.
You can create a design response that uses damage only in a shape optimization, and it can be used only as an objective function—minimization of the maximum damage in the critical areas. The Optimization module provides damage values as equivalent stress values. You can create a damage design response where the durability analysis runs only once in the optimization loop. Alternatively, you can create a damage design response when the durability analysis contains load case information and runs multiple times in the optimization loop.
| Abaqus/CAE Usage: | Optimization module: Task |
Optimization module: Task |
In most optimization problems you will use displacement and/or rotation to define your objective function or constraints. For example, the maximum displacement of a vertex could be either an objective or a constraint of an optimization. The performance of the optimization is improved if you apply displacements and rotations to only vertices or to small regions. In addition, performance is improved if you assign regions that are used to define displacements or reactions as frozen regions (the Optimization module will not remove elements from frozen regions during the optimization).
Table 13.2.1–1 lists the available displacement and rotation variables.
Table 13.2.1–1 Displacement and rotation variables for a general and sizing topology optimization.
| Displacement | Rotation | |
|---|---|---|
| i-direction | ||
| Absolute | ||
| Absolute in i-direction |
| Abaqus/CAE Usage: | Optimization module: Task |
The energy stiffness is a measure that has no physical meaning but can be used as an objective function or a constraint in an optimization to optimize the stiffness of a structure that is subjected to both external loading and prescribed displacements.
To optimize the stiffness of a structure with only external loading, the strain energy should be minimized:
![]()
In contrast, if a load case is driven by prescribed displacements, the elastic energy, or compliance, will decrease only if the structure is made softer. To optimize a structure with only prescribed displacements, the strain energy should be maximized:
![]()
The strain energy with both external loads and prescribed displacements is given as
![]()
The energy stiffness measure is used only for optimization (it has no physical meaning) and is given as
![]()
You cannot use the energy stiffness measure as a design response in a model that is experiencing thermal loading or mass-dependent loading, such as gravity. An energy stiffness design response must be applied to the entire model. When energy stiffness is used as an objective function, you must select a target that tries to minimize the sum of the weighted differences between the design response and the reference value, regardless of whether an external load and/or prescribed displacements are being applied to the structure.
| Abaqus/CAE Usage: | Optimization module: Task |
If your model is undergoing large deformations, a measure of the stress is not always a good indicator of the model's response. For example, a structure undergoing plastic deformation will, for an ideal plastic material, experience a large constant stress over the plastic area. In these circumstances a measure of the strain is a more reliable indicator of the model's response. You can choose from the following equivalent strains:
Elastic
Plastic
Total (the sum of the elastic and plastic)
| Abaqus/CAE Usage: | Optimization module: Task |
Equivalent stresses are the most commonly used objective function of a shape optimization. All of the stress values that are calculated by the Optimization module, whether nodal or from Gauss points or elements, are interpolated to the nodes. For example, you can try to optimize your model with an objective function that tries to minimize the maximum von Mises stresses in a region with stress concentrations or tries to minimize contact pressure in a region with contact. The Optimization module considers only the maximum value of an equivalent stress within a region. The Optimization module issues warnings for nodes that do not have the appropriate stress values. For example, if you select an objective response of contact stress, the Optimization module issues warnings about nodes of elements that are not in contact. If your Abaqus model contains multiple load cases, the design response is evaluated by summing the stress values from each load case.
You can choose from the following equivalent stresses:
von Mises
Maximum principal and absolute maximum principal
Minimum principal and absolute minimum principal
Second principal
Beltrami
Drucker Prager
Galilei
Kuhn
Mariotte
Mises
Sandel
Sauter
Tresca
Contact stress pressure
Total shear contact stress
Shear contact stress in the 1-direction
Shear contact stress in the 2-direction
Total contact stress
| Abaqus/CAE Usage: | Optimization module: Task |
You can use nodal internal forces and moments of the whole model or a region of the model as an objective function or a constraint in a general topology or sizing optimization.
Table 13.2.1–2 lists the available nodal internal force and moment variables.
Table 13.2.1–2 Nodal internal force and moment variables for a general and sizing topology optimization for the elements e attached to the nodes i.
| Nodal internal force | Nodal internal moment | |
|---|---|---|
| i-direction | ||
| Absolute | ||
| Absolute in i-direction |
You must use the global coordinate system with an absolute internal force or with absolute internal moment. Your structure must have stiffness in the direction of the force used in the optimization; otherwise, the internal force will be zero in this direction.
| Abaqus/CAE Usage: | Optimization module: Task |
Modal eigenvalues are the simplest dynamic responses in structural analysis. Typical uses of data from an eigenfrequency analysis during a topology optimization include the following:
maximize the lowest eigenfrequencies,
maximize a selected eigenfrequency,
constrain an eigenfrequency to be higher or lower than a given value,
maximize or minimize an eigenfrequency at a certain mode, and
perform a bandgap optimization that force modes away from a certain frequency.
The Optimization module supports two approaches for optimizing the eigenfrequencies:
single eigenfrequencies from modal analysis and
the Kreisselmaier-Steinhauser formulation.
The Kreisselmaier-Steinhauser formulation is the more efficient of the two approaches and should be used whenever possible. The only advantage of optimizing single eigenfrequencies is that you can use the sum of the eigenfrequencies as a constraint in a general topology or sizing optimization, which you cannot do with the Kreisselmaier-Steinhauser formulation.
When you are trying to maximize the lowest eigenfrequency, it is recommended that you consider not only the first eigenfrequency but also at least the next two highest natural frequencies. During the optimization, the various natural frequencies are weighted by their distance from the lowest natural frequency—the closer a natural frequency approaches the first natural frequency during the optimization, the more it is weighted. You should use the Kreisselmaier-Steinhauser eigenvalue formulation if you are trying to maximize the lowest eigenfrequency or, in particular, if you are trying to maximize more than one of the lowest eigenfrequencies. You do not need to use mode tracking if you are using the Kreisselmaier-Steinhauser formulation to maximize the lowest eigenfrequency, but you should use mode tracking for the higher modes because the modes might switch. For example, while the model is being optimized, the frequency of the first mode is maximized and the second eigenmode can become the mode with the lowest frequency.
| Abaqus/CAE Usage: | Optimization module: Task |
You can use a moment of inertia design response in an optimization to minimize the rotational inertia about a selected axis. You can use the sum of the moment of inertia of the whole model or a region of the model as an objective function or a constraint in a general topology or sizing optimization.
You can choose the moment of inertia in the three principal directions or the three principal planes:
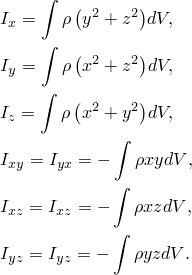
If you select a local coordinate system, the Optimization module uses the direction of the axes to recalculate the center of gravity. The Optimization module applies the global coordinate system if you do not select a local coordinate system.
When the Optimization module calculates the moment of inertia, it treats shell and membrane regions as three-dimensional regions by applying the thickness of the region. The Optimization module calculates the moment of inertia using only the element types that are supported by topology optimization. As a result, the moment of inertia calculated by the Optimization module might not be the same as the moment of inertia calculated by Abaqus/Standard or Abaqus/Explicit; for example, if your model contains beam or truss elements (wire regions in Abaqus/CAE).
The moment of inertia with respect to any two orthogonal axes is zero if you have selected either of the axes to be an axis of symmetry.
| Abaqus/CAE Usage: | Optimization module: Task |
The nodal strain energy density, ![]() , is a local point-wise strain energy that can provide a better representation of failure than stresses in nonlinear materials.
, is a local point-wise strain energy that can provide a better representation of failure than stresses in nonlinear materials.
| Abaqus/CAE Usage: | Optimization module: Task |
Nodal reaction forces and moments can be used as a design response only in general and sizing topology optimization. As with displacements, the performance of the optimization is improved if you apply reaction forces or moments to only vertices or to small regions and assign those regions as frozen regions (the Optimization module will not remove elements during the optimization).
Table 13.2.1–3 lists the available nodal reaction force and moment variables.
Table 13.2.1–3 Nodal reaction force and moment variables for a general and sizing topology optimization for the elements e attached to the nodes i.
| Nodal reaction force | Nodal reaction moment | |
|---|---|---|
| i-direction | ||
| Absolute | ||
| Absolute in i-direction |
You cannot use a reference coordinate system with an absolute reaction force or with an absolute reaction moment. Your structure must have stiffness in the direction of the force used in the optimization; otherwise, the reaction force will be zero in this direction.
| Abaqus/CAE Usage: | Optimization module: Task |
You can use the scaled element centroidal von Mises stress of the whole model or a region of the model as an objective function in an optimization. You must avoid regions with stress singularities caused by external loads or boundary conditions.
The scaled element centroidal von Mises stress is defined as
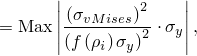
The von Mises stress is calculated at the centroid of the element to avoid stress singularities that might be present in the initial model or might appear in an optimized structure before it is smoothed. You cannot compare the scaled element centroidal von Mises stress with the von Mises stress calculated by Abaqus. The two measures are equal only when the element is solid and has a relative density of 1.0.
You can provide the reference stress when you create the objective function, or the Optimization module can calculate the reference stress during the initial optimization iteration. If you provide the reference stress, the value should not be too low or numerical singularities will result. The reference stress is given as
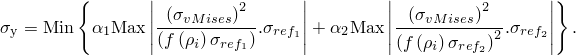
You can define multiple load cases for the scaled element centroidal von Mises stress measure. Static linear analysis is supported. Static nonlinear analysis supports only contact nonlinearities. Nonlinear materials and geometrical nonlinearities, such as large deformations, are not supported.
| Abaqus/CAE Usage: | Optimization module: Task |
The compliance of a structure is a measure of its overall flexibility or stiffness and is defined as the sum of the strain energy of all the elements, ![]() for linear models, where
for linear models, where ![]() is the displacement vector and
is the displacement vector and ![]() is the global stiffness matrix. Compliance is the reciprocal of stiffness, and minimizing the compliance is equivalent to maximizing the global stiffness. If a load case is driven by forces or pressures, you should choose to minimize the strain energy to maximize the global stiffness. However, if a load case is driven by a thermal field, strain energy decreases when the optimization modifies the structure to make it softer. As a result, you should always choose to maximize the strain energy because attempting to minimize the strain energy can result in a stiff structure. In addition, you should always choose to maximize the strain energy if prescribed displacements are applied to your model.
is the global stiffness matrix. Compliance is the reciprocal of stiffness, and minimizing the compliance is equivalent to maximizing the global stiffness. If a load case is driven by forces or pressures, you should choose to minimize the strain energy to maximize the global stiffness. However, if a load case is driven by a thermal field, strain energy decreases when the optimization modifies the structure to make it softer. As a result, you should always choose to maximize the strain energy because attempting to minimize the strain energy can result in a stiff structure. In addition, you should always choose to maximize the strain energy if prescribed displacements are applied to your model.
Topology optimization considers the total strain energy for all of the elements; therefore, if you choose strain energy as an objective function, you must apply the objective to the entire model. You cannot use strain energy as a constraint in your optimization.
| Abaqus/CAE Usage: | Optimization module: Task |
The volume is defined as the sum of the volume of the elements in the design area, ![]() , where
, where ![]() is the element volume. During a topology optimization, the elements are scaled with the current relative density defined in your Abaqus model. For most optimization problems, you must apply a volume constraint. For example, if you are trying to minimize the strain energy (maximize the stiffness) and do not apply a volume constraint, the Optimization module simply fills the entire design area with material.
is the element volume. During a topology optimization, the elements are scaled with the current relative density defined in your Abaqus model. For most optimization problems, you must apply a volume constraint. For example, if you are trying to minimize the strain energy (maximize the stiffness) and do not apply a volume constraint, the Optimization module simply fills the entire design area with material.
| Abaqus/CAE Usage: | Optimization module: Task |
The weight is defined as the sum of the weight of all the elements in the design area, ![]() , where
, where ![]() is the element weight. The Optimization module scales elements using the current relative density. For most optimization problems, you must apply either a volume or a weight constraint. Using weight instead of volume allows you to constrain the optimized model to a specified physical weight and accounts for regions composed of materials with different densities. The Optimization module uses only supported element types when calculating the weight.
is the element weight. The Optimization module scales elements using the current relative density. For most optimization problems, you must apply either a volume or a weight constraint. Using weight instead of volume allows you to constrain the optimized model to a specified physical weight and accounts for regions composed of materials with different densities. The Optimization module uses only supported element types when calculating the weight.
| Abaqus/CAE Usage: | Optimization module: Task |

You must specify the operation that the Optimization module will use to arrive at a single scalar value for the design response, although some restrictions apply. For example, a volume design response can only use the sum of the volume within the design area. A design response that calculates the von Mises stress must use the maximum value of the stress within a region of the model. (None of the operators are relevant when the Optimization module calculates a dynamic frequency design response.) The following design response operators are provided by the Optimization module:
Minimum or maximum: The minimum or maximum value within the selected region. The Optimization module allows only the maximum operator for stress, contact stress, and strain design responses.
Sum: The sum of all the values within the selected area. The Optimization module allows only the sum operator for volume, weight, moment of inertia, and gravity design responses.

The design responses you can create are dependent on the type of structural optimization you are performing—topology, shape, sizing, or bead. The type of optimization also controls whether you can use a design response as an objective, as a constraint, or as both.
Table 13.2.1–4 Design responses for condition-based topology optimization.
| Design response | Objective | Constraint |
|---|---|---|
| Strain energy | ||
| Volume |
Table 13.2.1–5 Design responses for general topology optimization.
| Design response | Objective | Constraint |
|---|---|---|
| Center of gravity | ||
| Displacement and rotation | ||
| Eigenfrequency from Kreisselmaier-Steinhauser formula | ||
| Eigenfrequency from modal analysis | ||
| Energy stiffness measure | ||
| Internal and reaction forces and moments | ||
| Moment of inertia | ||
| Scaled centroidal von Mises stress | ||
| Strain energy | ||
| Volume | ||
| Weight |
Table 13.2.1–6 Design responses for shape optimization.
| Design response | Objective | Constraint |
|---|---|---|
| Contact stress | ||
| Damage | ||
| Eigenfrequency from Kreisselmaier-Steinhauser formula | ||
| Equivalent strain | ||
| Equivalent stress | ||
| Nodal strain energy density | ||
| Volume | ||
| Weight |
Table 13.2.1–7 Design responses for sizing optimization.
| Design response | Objective | Constraint |
|---|---|---|
| Center of gravity | ||
| Displacement and rotation | ||
| Eigenfrequency from Kreisselmaier-Steinhauser formula | ||
| Eigenfrequency from modal analysis | ||
| Energy stiffness measure | ||
| Internal and reaction forces and moments | ||
| Moment of inertia | ||
| Strain energy | ||
| Volume | ||
| Weight |

You can define a design response that is a combination of the single values generated by multiple design responses; for example, you can add values or find the maximum of several values. You can also define a design response that is the result of an operation on another design response; for example, the difference between the value of the design response at different nodes.
For example, you can create two design responses that correspond to the displacement in the 1-direction of two selected vertices. Alternatively, you can create a design response that is the difference between the displacement in the 1-direction of two selected vertices. You can then define a constraint that forces the design response to be close to zero. In effect, the constraint forces the two selected vertices to move together in the 1-direction.
| Abaqus/CAE Usage: | Optimization module: Design Response |

Bakhtiary, N., P. Allinger, M. Friedrich, F. Mulfinger, J. Sauter, O. Müller, and J. Puchinger, “A New Approach for Size, Shape and Topology Optimization,” SAE International Congress and Exposition, Detroit, Michigan, USA, February 26–29, 1996.
Bendsøe, M. P., E. Lund, N. Ohloff, and O. Sigmund, “Topology Optimization - Broadening the Areas of Application,” Control and Cybernetics, vol. 34, pp. 7–35, 2005.
Bendsøe, M. P., and O. Sigmund, Topology Optimization: Theory, Methods and Applications, Springer-Verlag, Berlin Heidelberg New York, 2003.
Bendsøe, M. P., and O. Sigmund, “Material Interpolations in Topology Optimization,” Archive of Applied Mechanics, vol. 69, pp. 635–654, 1999.
Clausen, P. M., and C. B. W. Pedersen, Non-Parametric Large Scale Structural Optimization, ECCM 2006 III European Conference on Computational Mechanics, Lisbon, Portugal, June 5–9, 2006.
Cook, R. D., D. S. Malkus, and M. E. Plesha, Concepts and Applications of Finite Element Analysis, John Wiley & Sons Inc., 1989.
Emmrich, D., “Entwicklung einer FEM-basierten Methode zur Gesaltung von Sicken für biegebeanspruchte Leitstützstrukturen im Konstruktionsprozess,” Forschungsberichte des Instituts für Produktentwicklung, 13. Karlsruhe, 2004.
Hansen, L. V., “Topology Optimization of Free Vibrations of Fiber Laser Packages,” Structural and Multidisciplinary Optimization, vol. 29(5), pp. 341–348, 2005.
Olhoff, N., and J. Du, Topology Optimization of Vibrating Bi-Material Plate Structures with Respect to Sound Radiation, IUTUAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives, M. P. Bendsøe, N. Olhoff, and O. Sigmund, eds., pp. 147–156, Springer, 2006.
Pedersen, C. B. W., and P. Allinger, Industrial Implementation and Applications of Topology Optimization and Future Needs, IUTUAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives, M. P. Bendsøe, N. Olhoff, and O. Sigmund, eds., pp. 147–156, Springer, 2006.
Sigmund, O., and J. S. Jensen, “Systematic Design of Phononic Band Gap Materials and Structures by Topology Optimization,” Philosophical Transactions of the Royal Society: Mathematical, Physical and Engineering Sciences, vol. 361, pp. 1001–1019, 2003.
Stolpe, M., and K. Svanberg, “An Alternative Interpolation Scheme for Minimum Compliance Optimization,” Structural and Multidisciplinary Optimization, vol. 22, pp. 116–124, 2001.
Svanberg, K., “The Method of Moving Asymptotes—A New Method for Structural Optimization,” International Journal for Numerical Methods in Engineering, vol. 24, pp. 359–373, 1987.