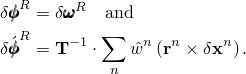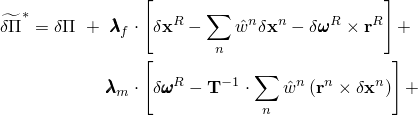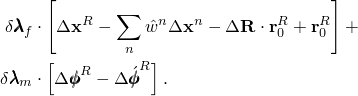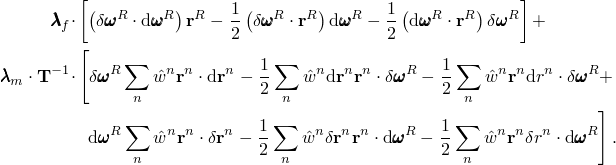Products: Abaqus/Standard Abaqus/Explicit
Distributing coupling constraints provide a means to connect a reference node to a group of coupling nodes in a way that distributes loads according to weight factors that are prescribed individually at each coupling node. The constraints distribute forces and moments at the reference node as a coupling node–force distribution only.
The formulation presented here is used for the distributing coupling elements that are available in Abaqus/Standard, as well as the surface-based distributing coupling and fastener constraints that are available in both Abaqus/Standard and Abaqus/Explicit. For the surface-based distributing coupling and fastener constraints, this section defines the load distribution relationship for the default continuum coupling method.
The reference node has displacement 
and rotation 
degrees of freedom. Only the displacement 
degrees of freedom of the coupling nodes are active in this constraint. Each coupling node has a weight factor 
assigned, which determines the proportion of load carried by the constraint that is transmitted through the coupling node. Weight factors are dimensionless, and their magnitude is significant only in a relative sense. Hereafter, normalized weights are used:
Let 
and 
be the load and moment applied to the reference node. The statically admissible force distribution 
among the coupling nodes satisfies
and 
are the positions of the reference and coupling nodes, respectively. For an arbitrary number of coupling nodes there is no unique solution to Equation 3.9.8–1.The force distribution adopted in Abaqus has the property that the linearized motion of the reference node is compatible with the coupling node group motion in an average sense. This compatibility can be described by considering the momentum of a moving coupling node group in a case where weight factors are considered as masses. In this case the reference node motion is identical to that of a point on a rigid body occupying the position of the reference node, where the center of mass of the rigid body is the center of mass of the coupling nodes and the rigid body moves with the same linear and angular momentum as the coupling node group. Since the element mass is distributed this way, the dynamic behavior of the element also has this property.
is the second-order identity tensor. This force distribution is recognized to be equivalent to the classic bolt-pattern force distribution when the weight factors are interpreted as bolt cross-section areas.The load distribution results in the following linearized constraint on node motions:
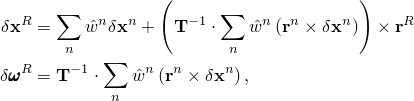
.Finite displacement and rotation terms take the form of a constraint on the motion of the reference node as a function of the coupling-node finite incremental motions. A measure of the finite rotation of the coupling node arrangement is developed first and is based on the mid-increment position of the coupling nodes, defined as
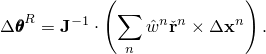
The finite incremental rotation tensor 
is deduced from the above expression according to the Hughes and Winget (1980) formula,
This orthogonal tensor yields an incremental finite-rotation vector 
. From this rotation description comes the constraint expressions for finite displacement and rotation:
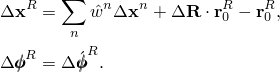
The virtual work expression for the attached structure is augmented with the contribution of the constraint
where
is the augmented virtual work expression, 
is the virtual work expression for the attached structure, and 
and 
are the respective Lagrange multiplier variables for force and moment.The initial stress stiffness terms are derived from a suitable approximation of the exact virtual work expression shown in Equation 3.9.8–2. This approximation is based on an assumption of infinitesimal incremental motions, 
and 
, that implies
